by cawan (cawan[at]ieee.org or chuiyewleong[at]hotmail.com)
on 03/11/2013
We all know about this equation
When we multiply an integer n with j, then it becomes nj. If we multiply nj with j again,
then it becomes –n. Again, if we multiply –n with j, it becomes –nj. If we multiply the
–nj with j again, then we get n. So, if we keep multiplying an integer with j, then we
get a repeating series, n, nj, -n, -nj, n, nj, -n, -nj, n,…
If we assume the j is residing at imaginary axis, which is orthogonal to the real axis in a
complex plane, then the repeating series can be plotted on the complex plane as a rotating
circle in anticlockwise. On the other hand, if the integer n keeps multiplying with –j
(instead of +j), then the rotating circle is in clockwise. Now, we need to prove the j is really
orthogonal to the real axis. If we define the real axis as x-axis and imaginary axis as y-axis,
for any point located at the complex plane can be expressed as (x, y). For the case of a circle
on the complex plane, if a point (x, y) rotates an angle θ in anticlockwise, the new point
(x1, y2) can be expressed as
On the other hand, if we represent (x, y) as a complex number, x+jy, and multiply it with
e^(jθ) , then what will happen? Well, Euler’s equation told us
So,
Apparently, equation (5) is matching to equation (2) and (3). Thus, we can say that now
for any point (x, y) located at a complex plane, if the point rotates an angle θ in anticlockwise,
then the new point (x1, x2) can be obtained by multiplying (x, y) with e^(jθ) . For the same
reason, if a point at real axis rotates 90° in anticlockwise, then the point should multiply with
e^(j(π/2)) in order to get to the new point. If we express e^(j(π/2)) in polar form, then
Well, now there is no issue for imaginary axis is always orthogonal to the real axis. However,
while a point keep rotating as a circle in a complex plane, then the number of cycle being
completed for a full circle in one second is defined as frequency in the unit of radians per
second, ω. So,
Where the unit of f is in Hz. So now,
From (10) and (11), we know that a complex sinusoidal signal will comprise of two sinusoidal
signals in same frequency but with 90° of phase difference. However, in practical, we normally
deal with real number signal, instead of complex signal. For the case of cos(ωt), it can be expressed
in exponential form.
From (12), it shows a real number frequency will comprise of a positive and a negative complex
frequencies, which is well known as even symmetry of magnitude spectrum. If there is a signal
with center frequency at f1 multiply with cos(2πf1t), then we can two signals with different center
frequency, 2f1 and 0. So, if we use a low pass filter to remove 2f1 from the product signal, then
we can get a signal with center frequency at 0 Hz. In software-defined radio (SDR), such approach
is useful for analog to digital converter (ADC) to sample high frequency signal. Now, how about
sin(ωt)? Well, it can be expressed in exponential form too.
From (13), it shows for any signal which multiply with sin(ωt), it will be turned into imaginary axis
(because it is multiplying with j). As similar to cos(ωt), sin(ωt) also comprises of a positive and a
negative frequencies. However, the positive frequency would have a negative magnitude spectrum as
oppose to negative frequency, which is well known as odd symmetry. When we multiply a signal with
sin(ωt) where the ω is equal to the center frequency of the signal, we can bring the signal to 0 Hz as
center frequency. In additional, since there is a j come together with sin(ωt), while multiplying the
signal with sin(ωt), the spectrum of the signal with 0 Hz as center frequency is actually located at the
imaginary axis. As we know, the process of quadrature sampling is about to transform a real number
signal into a complex number signal. Thus, by multiplying a real number signal with cos(ωt) and
sin(ωt) in individual, after being processed by low pass filter, we get Re(t) and Im(t), respectively.
The Re(t) and Im(t) are sometimes defined as i(t) and q(t), respectively, where the i stand for in-phase
and the q stand for quadrature. Besides, both of them having half magnitude at center frequency of 0
Hz (we assume the original center frequency of the signal is identical to the ω). However, Im(t) is at
imaginary axis, which is orthogonal to the real axis, so, we need to twist it 90° in clockwise by
multiplying with -j to make it aligned to real axis. Whiles both of them with half magnitude are
superposed in real axis, they construct a full magnitude real number signal with 0 Hz as center
frequency. As a result, the complex number signal of a real number signal x(t) can be expressed as
x(t)cos(ωt) -jx(t)sin(ωt). Someone might argue the x(t) should have its negative spectrum as it is a
real number signal, and we didn’t consider about the impact of positive spectrum of cos(ωt) and
sin(ωt) yet. Well, I leave that part as your own exercise to show the signals cancellation among them.
sin(ωt) yet. Well, I leave that part as your own exercise to show the signals cancellation among them.
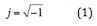

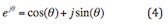






No comments:
Post a Comment